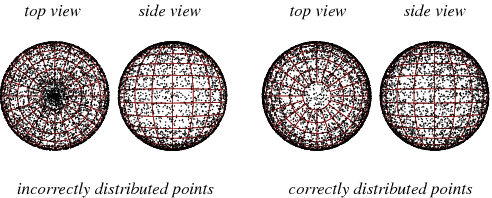
To pick a random point on the surface of a unit sphere, it is incorrect to select spherical coordinates 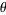 and
and 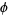 from uniform distributions
from uniform distributions 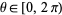 and
and ![phi in [0,pi]](http://mathworld.wolfram.com/images/equations/SpherePointPicking/Inline4.gif) , since the area element
, since the area element 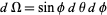 is a function of
is a function of 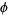 , and hence points picked in this way will be "bunched" near the poles (left figure above).
, and hence points picked in this way will be "bunched" near the poles (left figure above).
To obtain points such that any small area on the sphere is expected to contain the same number of points (right figure above), choose 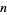 and
and 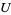 to be random variates on
to be random variates on 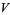 . Then
. Then
| (1) | |||
| (2) |
gives the spherical coordinates for a set of points which are uniformly distributed over 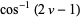 . This works since the differential element of solid angle is given by
. This works since the differential element of solid angle is given by
Weisstein, Eric W. "Sphere Point Picking." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SpherePointPicking.html
No comments:
Post a Comment